数学前导后不导加后导前不导什么意思
在数学中,导数是一个非常重要的概念,它表示函数在某一点的切线斜率。导数的存在意味着函数在该点是可微的,即存在一个常数,使得函数在该点的切线与x轴的交点为0。
导数的正负性也决定了函数在该点的增减性。然而,在某些情况下,我们可能无法直接求出函数在某一点的导数,这时就需要利用一些间接的方法来求解。

其中,“前导后不导加后导前不导”是一种常见的间接求导方法。
这种方法的基本思想是:如果函数在某一点的前导数存在,且后导数不存在;或者函数在某一点的后导数存在,且前导数不存在,那么我们可以分别对这两部分进行求导,然后将结果相加或相减,从而得到原函数在该点的导数。
具体来说,假设我们要求解的函数为f(x),已知在某一点a处的前导数为f'(a),后导数为f''(a)。我们可以先求出f(a+h)和f(a-h)的值,然后分别计算它们的差分商,得到f(a+h) - f(a-h) / 2h。
这样,我们就得到了f(a)在小区间[a-h, a+h]上的近似导数值。由于h是一个非常小的正数,所以这个近似值可以看作是f(a)在点a处的导数的一个近似值。
需要注意的是,这种方法只能给出一个近似值,而不是精确值。因此,在实际问题中,我们需要根据具体情况来判断这种方法是否适用,以及如何选择合适的h值。

此外,这种方法还存在一定的局限性,例如当函数在某一点处不连续时,就无法使用这种方法来求解导数。
总之,“前导后不导加后导前不导”是一种常用的间接求导方法,它可以帮助我们在某些情况下求解函数在某一点的导数。然而,这种方法也有一些局限性,需要我们在实际应用中加以注意。
相关阅读
-

去除和除以是数学中两个不同的概念,它们之间存在一定的区别。去除是一种减法运算,而除以是一种除法运算。去除和除以在实际应用中非常广泛,它们可以帮助我们进行各种数值计算。了解去除......
2024-04-23 1122 -

做题慢与智商无关,而是由于学习方法不当、缺乏兴趣、缺乏耐心等原因导致的。要提高数学速度,需要从选择合适的学习方法、培养对数学的兴趣、培养耐心、加强练习和总结经验教训等方面入手......
2024-04-23 6540 -

诺贝尔数学奖没有数学奖的原因可能有很多,包括数学与科学、文学、和平等领域之间的界限不够明确,以及诺贝尔数学奖的评选标准可能过于严格等。然而,这并不意味着数学与科学、文学、和平......
2024-03-05 1251 -

这个问题可以通过向量的概念来解决。向量是一个有方向的量,可以用来表示空间中的一点到另一点的距离或者方向。在这个问题中,我们可以利用向量的性质来判断四个点是否在同一个平面上。...
2024-02-22 9715 -
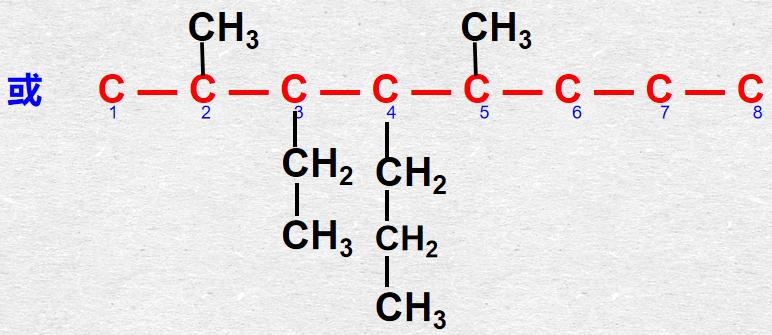
结构和简式都是用来描述有机化合物的结构的重要工具。它们各有优点和缺点,适用于不同的场合。对于需要全面理解化合物结构的情况,我们需要使用结构式;而对于只需要快速理解化合物结构的......
2024-04-23 7587 -

总之,水滴石穿是一个既具有化学变化特点,又具有物理变化特点的现象。它的发生原因主要是由水滴和石头的性质以及它们之间的相互作用方式所决定的。虽然水滴石穿是一个古老的寓言故事,但......
2024-04-23 3056 -

总之,掌握显微镜的使用方法步骤及注意事项,对于提高观察效果和保护眼睛健康具有重要意义。希望本文能帮助您更好地理解和使用显微镜。...
2024-04-23 8009 -

从专业特点、就业前景和工作环境等方面来看,影像学、检验学和护理学三个专业都具有一定的优势。然而,具体选择哪个专业还需要根据个人的兴趣、特长和职业规划来决定。对于女生来说,可以......
2024-04-23 2658 -

总的来说,动员大会是一种重要的学校活动,它可以鼓励学生积极参与学习,提高他们的学术表现,并激发他们对未来的激情和期待。通过这种类型的会议,学校可以向学生传达他们的目标和期望,......
2024-04-23 8994 -

去除和除以是数学中两个不同的概念,它们之间存在一定的区别。去除是一种减法运算,而除以是一种除法运算。去除和除以在实际应用中非常广泛,它们可以帮助我们进行各种数值计算。了解去除......
2024-04-23 1122
发表评论

